Final exam math using python for calculates result.
លំហាត់
We use Jupyter Notebook in anaconda, and you can use python online ide for run simulations.
1. Result
Exercises 8
Source code combine exercise 8
def calculate_determinant(matrix):
dimension = len(matrix)
if dimension == 1:
return matrix[0][0]
determinant = 0
for col in range(dimension):
sub_matrix = [[0] * (dimension - 1) for _ in range(dimension - 1)]
for i in range(1, dimension):
curr_col = 0
for j in range(dimension):
if j != col:
sub_matrix[i - 1][curr_col] = matrix[i][j]
curr_col += 1
sub_determinant = calculate_determinant(sub_matrix)
determinant += ((-1) ** col) * matrix[0][col] * sub_determinant
return determinant
def get_cofactor(matrix, row, col):
return [row[:col] + row[col + 1:] for row in (matrix[:row] + matrix[row + 1:])]
def calculate_adjoint(matrix):
dimension = len(matrix)
adj = [[0] * dimension for _ in range(dimension)]
for i in range(dimension):
for j in range(dimension):
cofactor = get_cofactor(matrix, i, j)
adj[j][i] = ((-1) ** (i + j)) * calculate_determinant(cofactor)
return adj
def calculate_inverse(matrix):
det = calculate_determinant(matrix)
if det == 0:
print("Singular matrix, can't find its inverse")
return None
dimension = len(matrix)
inv = [[0] * dimension for _ in range(dimension)]
adj = calculate_adjoint(matrix)
for i in range(dimension):
for j in range(dimension):
inv[i][j] = adj[i][j] / det
return inv
def display(matrix):
for row in matrix:
print(" ".join(str(num) for num in row))
def enter_matrix():
dimension = int(input("Enter the dimension of the matrix: "))
matrix = []
for i in range(dimension):
row = []
for j in range(dimension):
while True:
try:
element = int(input(f"Enter element at position a{i+1}{j+1}: "))
break
except ValueError:
print("Invalid input. Please enter a numeric value.")
row.append(element)
matrix.append(row)
return matrix
def gaussian_elimination(matrix):
dimension = len(matrix)
augmented_matrix = []
for i in range(dimension):
row = list(matrix[i]) + [1 if j == i else 0 for j in range(dimension)]
augmented_matrix.append(row)
for i in range(dimension):
pivot_row = i
for j in range(i + 1, dimension):
if abs(augmented_matrix[j][i]) > abs(augmented_matrix[pivot_row][i]):
pivot_row = j
augmented_matrix[i], augmented_matrix[pivot_row] = augmented_matrix[pivot_row], augmented_matrix[i]
pivot = augmented_matrix[i][i]
augmented_matrix[i] = [elem / pivot for elem in augmented_matrix[i]]
for j in range(dimension):
if j != i:
factor = augmented_matrix[j][i]
augmented_matrix[j] = [elem - factor * augmented_matrix[i][idx] for idx, elem in
enumerate(augmented_matrix[j])]
inverse = [row[dimension:] for row in augmented_matrix]
return inverse
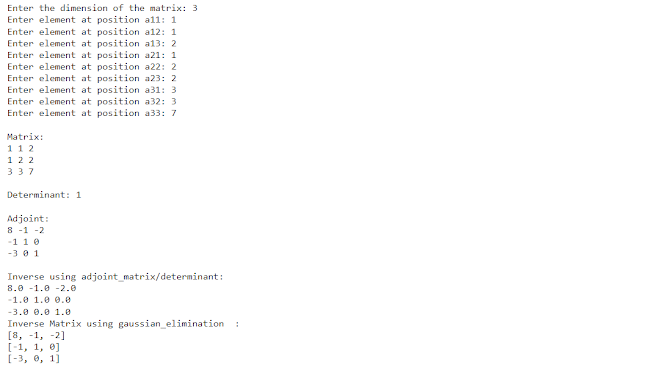
while True:
try:
matrix = enter_matrix()
print("\nMatrix:")
display(matrix)
determinant = calculate_determinant(matrix)
print("\nDeterminant:", determinant)
print("\nAdjoint:")
adjoint_matrix = calculate_adjoint(matrix)
display(adjoint_matrix)
print("\nInverse using adjoint_matrix/determinant:")
inverse_matrix = calculate_inverse(matrix)
if inverse_matrix is not None:
display(inverse_matrix)
inverse_matrix_ge = gaussian_elimination(matrix)
for i in range(len(inverse_matrix_ge)):
for j in range(len(inverse_matrix_ge[i])):
inverse_matrix_ge[i][j] = round(inverse_matrix_ge[i][j])
print("Inverse Matrix using gaussian_elimination :")
for row in inverse_matrix_ge:
print(row)
except ValueError:
print("Invalid matrix input. Please enter numeric values only.")
Exercises 9
1. Calculate crammer's rule
def calculate_determinant(matrix):
# for 2x2 matrix
if len(matrix) == 2:
determinant_2x2 = matrix[0][0] * matrix[1][1] - matrix[0][1] * matrix[1][0]
return determinant_2x2
determinant_ndimension = 0
for k in range(len(matrix)):
sign = (-1) ** k
sub_matrix = [row[:k] + row[k+1:] for row in matrix[1:]]
sub_det = calculate_determinant(sub_matrix)
determinant_ndimension += sign * matrix[0][k] * sub_det
return determinant_ndimension
def calculate_cramer(matrix, result):
determinant = calculate_determinant(matrix)
if determinant == 0:
return None # Unable to solve, determinant is zero
dimension = len(matrix)
solutions = []
for i in range(dimension):
modified_matrix = [row.copy() for row in matrix] # Create a copy of the original matrix
for j in range(dimension):
modified_matrix[j][i] = result[j]
solution = calculate_determinant(modified_matrix) / determinant
solutions.append(solution)
return solutions
def display(matrix):
print("Matrix:")
for row in matrix:
print(" ".join(str(num) for num in row))
def main():
try:
dimension = int(input("Enter the dimension of the matrix: "))
except ValueError:
print("Invalid input. Please enter a numeric value.")
return
matrix = []
print("Enter the matrix:")
for i in range(dimension):
row = []
for j in range(dimension):
variable = chr(ord('x') + j) # Convert 0-based index to variable label
while True:
try:
element = int(input(f"Simultaneous equation {i+1}, {variable}(a){i+1}{j+1}: "))
break
except ValueError:
print("Invalid input. Please enter a numeric value.")
row.append(element)
matrix.append(row)
result = []
print("Enter the result b of Simultaneous equation:")
for i in range(dimension):
variable = chr(ord('x') + i) # Convert 0-based index to variable label
while True:
try:
element = int(input(f"Enter result for equation b{i+1} of Simultaneous equation {i+1}: "))
break
except ValueError:
print("Invalid input. Please enter a numeric value.")
result.append(element)
display(matrix)
solutions = calculate_cramer(matrix, result)
if solutions is None:
print("Unable to solve the system of equations. Determinant is zero.")
else:
print("Solutions:")
for i, solution in enumerate(solutions):
variable = chr(ord('x') + i) # Convert 0-based index to variable label
print(f"{variable} = {solution}")
if __name__ == "__main__":
main()


0 comments:
Post a Comment